• Amal Augustine
• January 12, 2026

Effective Conceptual MCQs on Simple Harmonic Motion, Oscillations, and Wave Phenomena

Simple Harmonic Motion (SHM) and oscillatory motion form a crucial foundation in classical physics, appearing extensively in school boards, JEE, NEET, and university-level examinations. The questions discussed in this set revolve around restoring force, periodic motion, energy variation, damping, resonance, standing waves, and electromagnetic effects like eddy currents, all of which are interconnected through fundamental physical principles.

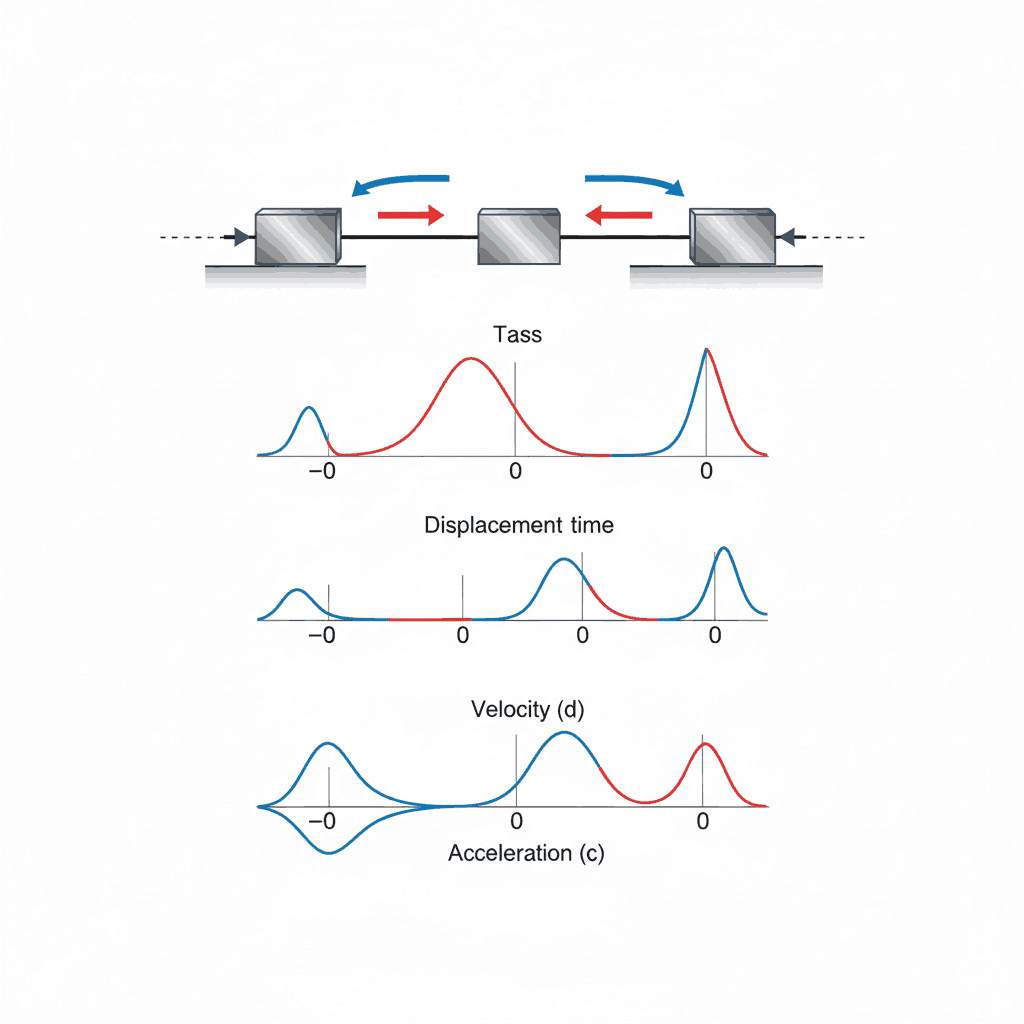
Many natural and artificial systems exhibit simple harmonic motion, such as a mass attached to a spring, oscillations of a pendulum for small angular displacements, vibrations of atoms in solids, and electrical oscillations in LC circuits. In Simple Harmonic Motion, physical quantities like displacement, velocity, and acceleration vary periodically with time, while the motion itself can be represented using sine or cosine functions. The governing differential equation of Simple Harmonic Motion highlights the importance of angular frequency, which determines how fast the system oscillates.

One of the key features of simple harmonic motion is the continuous exchange between kinetic energy and potential energy. At the mean position, the particle possesses maximum kinetic energy and zero potential energy, whereas at the extreme positions, kinetic energy becomes zero and potential energy reaches its maximum value. However, the total mechanical energy of an ideal Simple Harmonic Motion system remains constant, provided no damping forces such as friction or air resistance are present.

Motion in Simple Harmonic Motion and Restoring Forces

In linear Simple Harmonic Motion, the defining condition is that the restoring force is directly proportional to displacement and always directed towards the equilibrium position. This leads to acceleration being maximum at the extreme positions and zero at the mean position. Consequently, the velocity is maximum at the mean position, a concept repeatedly tested through graphical and numerical MCQs.

The differential equation

d2xdt2+ω2x=0\frac{d^2x}{dt^2} + \omega^2 x = 0dt2d2x​+ω2x=0

clearly shows that ω2\omega^2ω2 represents the restoring force per unit displacement, which determines the angular frequency of oscillation.

Energy in Simple Harmonic Motion

The total mechanical energy of an Simple Harmonic Motion system remains constant and is directly proportional to the square of the amplitude. While displacement, velocity, and acceleration vary periodically, total energy does not—making it a non-periodic quantity in Simple Harmonic Motion.

When amplitude changes, energy changes significantly:

• Doubling amplitude → Maximum velocity doubles

• Energy increases by a factor of four

Average velocity over a complete oscillation is zero, but average speed depends on amplitude and frequency, a subtle but important distinction frequently tested.

Pendulum, Swing, and Oscillation-Based Systems

Changes in configuration affect the time period:

• Sitting on a swing lowers the center of mass → time period decreases

• Standing up raises the center of mass → time period decreases further

The kinetic energy oscillates with frequency 2f, while displacement oscillates with frequency f. This explains why energy-related MCQs often involve doubled frequencies.

MCQs on Simple Harmonic Motion with Answers:

Conclusion on Simple Harmonic Motion

In conclusion, simple harmonic motion represents a perfect balance between mathematical simplicity and physical applicability. Its defining characteristic—the proportional restoring force—leads to predictable, periodic behavior that can be analyzed precisely using equations and graphs. By studying Simple Harmonic Motion, learners gain deep insight into how oscillatory systems behave under ideal conditions.

The importance of Simple Harmonic Motion extends far beyond textbook problems. It provides a conceptual bridge between mechanics, waves, acoustics, and even quantum physics. Real-world systems rarely perform perfect simple harmonic motion, but Simple Harmonic Motion serves as an excellent approximation for small oscillations and forms the starting point for understanding damping, resonance, and energy dissipation. The study of Simple Harmonic Motion also enhances problem-solving skills by strengthening the ability to interpret motion graphs, apply energy principles, and relate physical quantities logically.